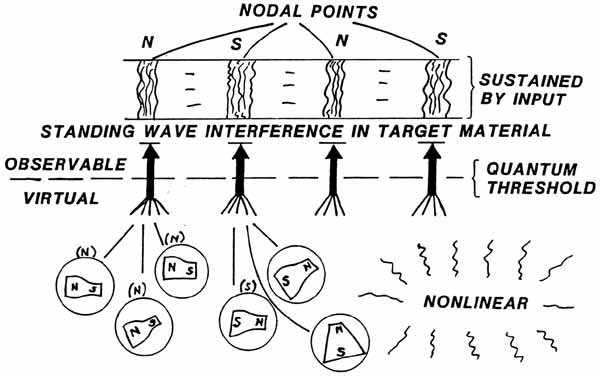
Now let us look at a non-linear case of the same sort of thing.  Now the bags are still around the little virtual magnets, but they are nonlinear.  This means that, to an observer outside the bag, one pole seems bigger or more powerful than the other. In other words, to the quantum observer, this bag appears to be a magnetic monopole at a point. 
          In the flux still on and off each observable spinning charged mass, we now have a steady component of "monopoles".  If we have a standing scalar wave present in a physical material in which the nonlinearity exists -- and the scalar waves can even be PRODUCING that nonlinearity -- we will have nodes available at which the monopoles will congregate and emerge and interact. 
          North monopoles will congregate at one node, while south monopoles will congregate at the next, and so on in alternating fashion. 
          That means that, at anyone node, monopoles of the same kind are steadily being "deposited" in the material.  These monopoles strongly repel each other, and so the material at that node is increasingly stressed in a tensile fashion. 
          Eventually the material will be torn apart at the node,
stress relieving the situation.  Movement of the material will release the nonlinear condition, stopping monopole production and deposit. However, at a break node, the same kind of magnetic pole will appear on each side of the break.
           That is, the breaks will be N-N, S-S, N-N, S-S, etc.
           An ordinary magnetic does not do that when it breaks.  Instead, it breaks N-S, N-S, etc.

Next Slide