On this slide we now show a simple way to make a scalar, zero-vector wave -- the kind of wave originally discovered by Nikola Tesla.
            It's simple.  We just believe that a sum-zero vector substructure makes a scalar quantity, and we MAKE some scalars that way.
           We also understand that a zero-gradient of a scalar is a zero vector, so that the scalar itself may be taken to be a zero vector.
           The simplest explanation of this wave is as follows:
           First, in physics we have two competing, mutually exclusive theories as to the nature of electromagnetic energy:  the wave theory and the particle theory.  Physicists argued for decades over these theories, for some experiments support one and some support the other.  They never solved the problem; they just agreed to quit arguing.  They formulated the "duality" principle to allow the saving of face to both sides.
           Briefly, the duality principle implies that, whatever the nature of electromagnetic energy is before an interaction, in the interaction you can get it to act as a wave or as a particle.  In other words, AS IT EXISTS, BEFORE THE INTERACTION, it is implicitly both particle and wave, joined together in some fashion, without being explicitly either one.
          With the fourth law of logic, this becomes perfectly clear.  With three-law Aristotlean logic, the problem is unresolvable.
           Let us use this idea of "explicit duality without implicit duality" to analyze the wave shown on the slide.
          First, from a wave aspect, the E-fields and the B-fields of the two waves do superpose and vectorially add.  Since the waves are 180 degrees out of phase, the exterior resultant wave has a zero electric field and a zero magnetic field.  Therefore it is a "zero-vector" wave, or "scalar" wave.  It's a wave of pure stress in spacetime.
          However, this scalar wave has a precisely determined substructure, consisting_of two ordinary sine waves, each of which comprises an ordinary E-H vector EM wave.
          Now we apply the photon consideration (remember, before we interact with the wave, it must implicitly possess BOTH wave and particle natures combined, and we have so far only examined the implication of the wave nature.
          The theory of photons' states that they are monocular critters.  Photons pass right through other photons without interaction, in a linear situation.  Therefore they can coexist without interaction, which is what we show here.
          One photon, by the way, is one wavelength .
          The photon theory requires that both substructure waves continue to exist as independent photons.  Therefore we are assured that our substructure is intact.
          However, notice that the totality of the two waves stresses spacetime.  In other words, we have twice the stress on spacetime now as we would have from either wave separately.
          This wave is therefore just a pure stress wave in spacetime itself.
          This thing oscillates time, oscillates the relativity of the situation, and can affect energy, time flow rate, inertia, gravity, etc. aspects of an absorbing system.
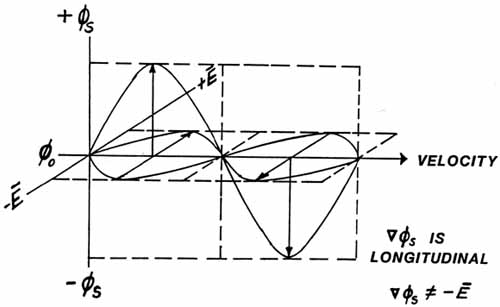
           Note that we have a rhythmic oscillation in phi (Ø), and we have a longitudinal stress wave, very similar to a sound wave.  The MEDIUM for this wave is the virtual particle flux that identically comprises vacuum spacetime itself.

Next Slide