|
-- THE SHADOW VECTOR --
Note that this spatial vector 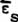 represents
represents 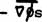 ,
that is, ,
that is,
|
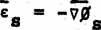
|
(18) |
but 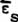 cannot be a force (mass system) vector. It can only exist as an
ordered pattern in the virtual flux between two separated points of the
vacuum; that is, as an ordered pattern in the virtual state.
Literally,
cannot be a force (mass system) vector. It can only exist as an
ordered pattern in the virtual flux between two separated points of the
vacuum; that is, as an ordered pattern in the virtual state.
Literally, 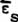 exists only as a tiny bit of order existing in great disorder.
exists only as a tiny bit of order existing in great disorder.
In other
words, the present EM theory is incorrect in stating that
|
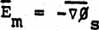
|
(19) |
in vacuum in the absence of an observable spinning
charged particle, since
|
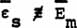
|
(20) |
The actual existence of 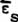 may be visualized in terms of successive differentials of
may be visualized in terms of successive differentials of 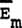 ,
broken into differentials ,
broken into differentials 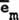 so small that, observably, each little differential's mass component m
has become virtual, so that
so small that, observably, each little differential's mass component m
has become virtual, so that
|
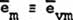
|
(21) |
where subscript m stands for mass, subscript v for
virtual, and observably
|
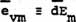
|
(22) |
but, in the absence of a spinning charged particle,
|
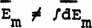
|
(23) |
since the 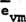 components remain individually separated. That is, in macro-time a
SHADOW force vector exists, made of microscopically ordered BUT UNJOINED
(unintegrated) "virtual state" vector differentials of what
would be an observable mass system force vector
components remain individually separated. That is, in macro-time a
SHADOW force vector exists, made of microscopically ordered BUT UNJOINED
(unintegrated) "virtual state" vector differentials of what
would be an observable mass system force vector 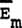 if integrated.
if integrated.
Thus, the
"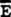 -vector" -vector"  that exists in vacuum is a "shadow" vector as shown in figure
12.
that exists in vacuum is a "shadow" vector as shown in figure
12.
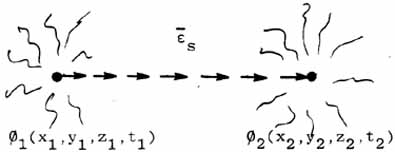
Figure 12. A "shadow vector" 
We
say that such a previous mass system vector, broken into ordered but
unjoined virtual vectors by the absenting of all mass, is a SHADOW
VECTOR, and we label it with a subscript vm, to represent "virtual
mass" system. To the macro observer, this is the kind of
"vector" that exists in vacuuo.
Note
that, observably, the shadow vector merely represents a special ordering
in Ñf.
It is NOT an OBSERVABLE (mass system) vector, but it IS an ordered
series of consecutive virtual vectors.
With each
virtual bit vector, a virtual time exists as well, and these
"virtual time bits" are also ordered consecutively (in
macrotime).
I point out
that any observable vector must be finite, and so it must have a finite
magnitude (finite length). In the simplest case, this length
ΔL is related to a Δt by
What I am saying is that ANY observable
spatial vector is actually a spatiotemporal vector, and the MAGNITUDE of
any vector is related to TIME (to the existence of that vector in time)
at the most fundamental level. Suffice it to say that, if the
fundamental quantum level (Δt) aspect of a vector is interfered
with, then the MAGNITUDE of the vector is interfered with.24 That
is, if we can make a time wave, we can change or affect ANY vector's
magnitude, including the magnitude of mass system vectors and charged
mass system vectors. Such a "time wave" can be made easily,
and it has been.
Next Page
|
